Avoir accès à une découpeuse laser est un must pour tout bricoleur… amateur de fabrication numérique. Les artisans qui aiment travailler la matière à la seule agilité de leurs mains (et je les respecte) ne seront donc pas intéressés par cet article.
La découpeuse laser est un merveilleux outil: elle permet de travailler avec précision et répétabilité, ce qui est très précieux dans la phase de prototypage. Mais encore faut-il savoir l’utiliser.
Cet article se concentre sur un assemblage bien précis, réalisable facilement avec une découpeuse laser: “l’enture à mi-bois en T”. Moi, j’appelle ça “par encoche”, ou “par rainure”, mais je ne suis pas ébéniste.
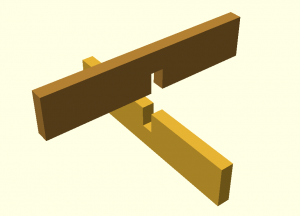
Il s’agit donc d’un simple emboîtement de 2 planches (ou panneaux), l’une dans l’autre, moyennant une rainure à mi-hauteur.
“Mais quelle difficulté à cela ?”, me direz-vous. Rien, tant que c’est à angle droit.
Ici, on va ajouter le calcul de la largeur de la rainure, en fonction de l’épaisseur de la planche, et de l’angle d’assemblage.
Formules
Comme la découpe des rainures est destinée à une découpeuse laser, il s’agit de découpe droite, perpendiculaire au plan du panneau.
Voici le schéma de l’assemblage, vu “du dessus”:
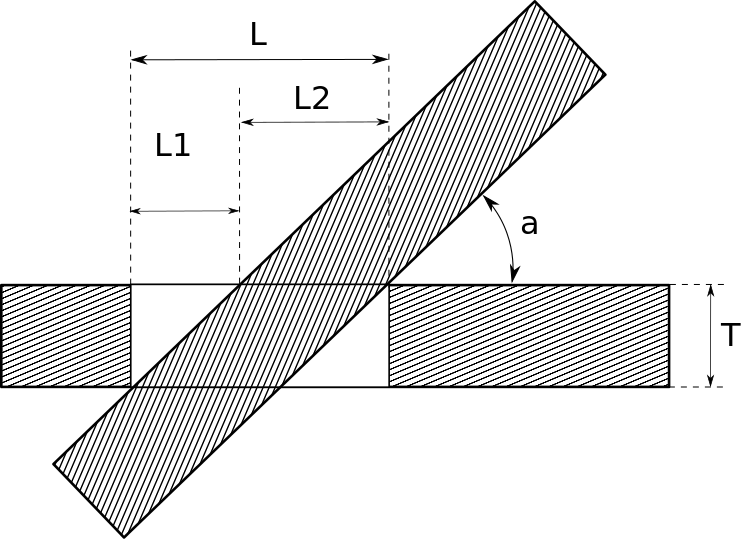
Légende:
- T: épaisseur des planches
- a: angle entre les 2 planches
- L: largeur des rainures
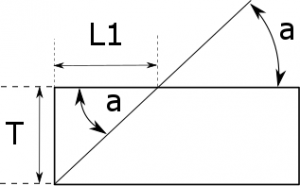On a donc, pour L1:
et donc:
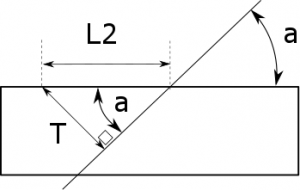et pour L2:
donc:
soit au total, pour L:
et donc:
On voit que pour un angle droit (90°): sin(90°) = 1, cos(90°) = 0, et on revient à la simple formule L=T
Et par exemple, pour un bois de 6mm d’épaisseur, avec un angle de 60 degrés:
Pour aller plus loin
Et si les planches sont d’épaisseur différentes ? (à suivre…)